Arquivos Matemática - DicasFree.com

julho 2, 2014

Raiz de número negativo, existe?

Raiz de número negativo

Por um tempão, vários matemáticos dedicaram suas vidas a descobrir a possibilidade de retirar raiz de números negativos. Alguns afirmavam que seria impossível tal feito, enquanto outros continuavam a tentar. Isso porque, em vista, é impossível retirar raiz de um número negativo.

Isso porque em números reais essa possibilidade se torna inexistente, pois os números que estão negativos, quando elevados ao quadrado, se tornam positivos. Em cálculos comuns, a raiz é extraída de um número inteiro quando ele é multiplicado por ele mesmo, ou seja:

√16 = 4

(raiz quadrada de 16 é igual a 4)

Sabemos isso, devido a multiplicação do número 4 vezes ele mesmo, ter resultado igual a 16.

Agora supomos que o número que aparece inteiro aqui, estivesse em estado negativo, ou seja:

√-16 = -4 x -4 = +16

Isso porque se calcularmos -4 x -4 o resultado seria: + 16

Ou seja, coerente com a matemática, os sinais de (-) x (-) é igual a +. Número que era negativo, se tornou positivo.

Tudo bem até aqui, mas essa não foi uma resposta válida para os matemáticos que continuaram suas pesquisas envolta do assunto. O que aconteceu então, foi a utilização de um número imaginário a √-1 que ficou simbolizado com a letra i, com isso seria possível fazer o cálculo de números negativos devido ao número imaginário.

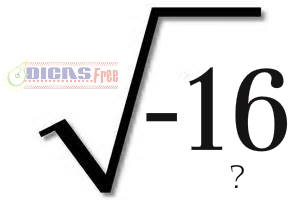
Entenda como ocorre o cálculo. — Raiz quadrada negativa

Agora para resolver uma raiz de número negativo, teremos o seguinte processo:

√-16 = √-1 x 16 =

√-1 x √-16 =

Ou seja:

√-1 = i

√16 = 4

Após tudo isso, foi possível resolver algumas equações de 2° grau. As equações foram sendo resolvidas baseadas exclusivamente em um novo conjunto numérico que surgia consequentemente de números complexos. Os números são basicamente constituídos em duas partes, sendo uma real e outra imaginária.

maio 14, 2014

Nomes usados para relacionar os ângulos

A trigonometria foi desenvolvida pelos seres humanos para uma infinidade de tarefas. Alguns acreditam que, originalmente, foram utilizadas para calcular o tempo através do relógio solar e mais tarde ser aplicada em construções mais complexas e na confecção de instrumentos de agrimensura.

A palavra trigonometria vem de termos gregos que traduzidos significam “medida do triângulo“, sendo quase exatamente o significado em questão. A trigonometria nada mais é do que a relação de comprimentos entre os lados de uma triângulo retângulo, perpassando os estudos geométricos.

Termos na Trigonometria

Para compreender melhor essa disciplina, é necessário aprender os significados dos termos para não ficar perdido no que os exercícios pedem. Para isso, disponibilizaremos uma lista de termos abaixo para que possa consultar na hora do sufoco. Confira:

Ângulo: é a união de duas retas em um único ponto;

Radiano: seria o arco cujo comprimento é equivalente ao comprimento ao raio da circunferência;

Grau: unidade de medida em uma circunferência. Equivale 1\360;

Ângulo Reto: é o ângulo em que a medida é de 90º;

Seno: seria a proporção entre o cateto oposto do ângulo e a hipotenusa do triângulo;

Coseno: seria a proporção entre o cateto adjacente do ângulo e a hipotenusa do triângulo;

Tangente: o resultado do cálculo da razão entre o seno e coseno de um triângulo;

Ângulo Raso: ângulos que quando mensurados, medem 180º;

Ângulo Agudo: ângulos que quando mensurados, medem entre oº a 90º;

Ângulo Obtuso: ângulos que quando mensurados, medem entre 90º a 180º;

abril 15, 2014

Decompor em fatores primos

Decomposição em fatores primos

A decomposição pode ser feita em qualquer número maior que 1. Esse pode ser decomposto facilmente em produtos de dois ou mais fatores. É necessário que durante a decomposição todos sejam feitos em fatores primos, eles são mais utilizados na soma ou subtração de uma fração.

Em alguns casos, é necessário que você encontre o máximo divisor e a partir de então consiga um conjunto de números para conseguir a decomposição dos mesmos em fatores primos. Há também alguns sites na internet que disponibilizam uma calculadora para a decomposição rápida.

Como fazer?

Antes de mais nada, é necessária uma linha vertical para que seja feita a decomposição. Vamos utilizar o número 45 como exemplo. É preciso que você procure um número que possa dividir em partes iguais, dando um resultado satisfatório, como o número 3.

Antes de continuar o processo, indicaremos quais os números primos mais utilizados:

» 2,3,5,7,11,13,17,19,23,29…

O número que encontramos para 45, no caso é o 3. Onde 45 é divido pelo 3, que resulta em 15, dando continuidade a equação. O quociente ( o número 3) é colocado do lado esquerdo da linha vertical que acabamos de indicar. Como sabemos, o resultado da divisão 15, encaixado logo abaixo o número 45.

Veja:

decompor 1

Esse processo acontece até que o quociente seja igual a 1. Ou seja, quando chegar nesse resultado, não necessitará de nenhum acréscimo ou divisão, considerando que somente os números maiores que 1, podem ser divididos e utilizados nessa mesma equação.

Veja:

decompor 2

O mais importante é que você descubra o quociente correto para decompor seu número. Procure sempre fazê-lo em números próximos que lhe darão um resultado satisfatório e inteiro. Ele deverá se dividir inteiramente até que seu resultado final seja 1, onde não há mais possibilidades de decomposição.

novembro 27, 2012dezembro 4, 2012

Como gostar de estudar matematica

Ábaco: A primeira “calculadora” inventada pelo homem.

A matética talvez seja a matéria mais odiada entre os alunos do ensino médio e fundamental. Por uma matéria estritamente relacionada a cálculos e inúmeros exercícios, os alunos acabam se abstendo de gostar e praticar corretamente tal disciplina.

Os métodos para ensinar a matemática também não são muito convidativos. Apenas passar as fórmulas e centenas de exercícios não despertará o interesse em todos os alunos, principalmente os que tendem a área das ciências humanas.

Para que o aluno goste e se interesse pelos assuntos matemáticos, o professor é de fundamental importância. Manter-se atualizado com os novos métodos e novas ferramentas de ensino pode ser um ótimo aliado para uma aula diferente, dinâmica e com maior aprendizado.

Uma das dicas é aliar o conhecimento matemático a história. Todo conhecimento matemático tem sua ligação a algum contexto histórico, com uma série de curiosidades e sua serventia. A explicação dessas áreas e promoção de atividades que buscam, por meio dos cálculos matemáticos, reconstruir as coisas da antiguidade podem muito bem despertar o interesse de grande parte dos alunos.

Usar a tecnologia a seu favor também pode ajudar a a tornar tudo mais interessante e agradável. Utilizar gráficos animados, datashow, jogos e outros recursos para demonstrar e aplicar os cálculos matemáticos já se revelou ser um método eficiente de aprendizado.

Se você já passou da época do ensino médio e ainda sim precisa de estudar matemática, procure informar-se mais sobre cada assunto, seu contexto histórico e sua utilidade. Ao fazer os cálculos, imagine a utilização real daquilo na prática e como era usado a muito tempo. Assista a vídeo aulas disponíveis na internet e busque preferencialmente exercícios com resolução para que você não se perca e se frustre com eventuais erros.

fevereiro 14, 2011agosto 27, 2013

Matemática 4 operações básicas e exercícios: Somar, Subtrair, Dividir e Multiplicar

As 4 operações básicas da matemática são essenciais para realizar qualquer cálculo imposto por uma questão, sendo ela relacionada a qualquer assunto. As regras desses sinais é o que faz dizer que algo pode estar certo ou errado em âmbito matemático.

Antes de mais nada é importante que a regra abaixo seja gravada, pois ela é essencial para realizar todos os tipos de contas.

Regra de sinais

+ com + = +

– com – = +

+ com – = –

– com + = –

Adição

A adição é o ponto de partida em aprendizagem dos cálculos. Ela soma tudo o que está separado e que queremos juntar. Esse processo pode ser dado por forma positiva e negativa. Veja abaixo:

* Exemplo 1

12+5+2=17

Como todos os sinais são positivos, a soma pode ser realizada de todas as maneiras, trocando os números de ordem, que o resultado sempre dará o mesmo.

* Exemplo 2

– 10+(-3)= -13

O -3 é colocado entre parenteses para que o sinal de adição e subtração não fique juntos. Para fazer esse cálculo, basta apenas observar a regra de sinais. No caso o cálculo acima pode ser representado também (analisando pela regra dos sinais) como:

-10-3=13

Subtração

A subtração corresponde a contas ou situações nas quais desejamos retirar uma quantidade de outra para visualizar o que irá sobrar.

* Exemplo 1

90-40=50

Na subtração, se fizermos a inversão dos números que permanecem antes do sinal de igualdade ou diminuir um número maior por outro maior, o resultado final iŕa possuir um valor negativo. Veja:

40-90=–50

Multiplicação

A multiplicação irá corresponder sempre a soma de parcelas iguais de qualquer número.

* Exemplo 1

5*5*5*5*5*5=30 ou 5*6=30 ou 6*5=30

A ordem dos números (ou fatores) nunca irá alterar o resultado da questão.

Todas as vezes em que surgir uma multiplicação em uma conta que possua somatórias ou subtrações, ela deverá ser realizada primeiro.

* Exemplo 2

2*(2+3+4)=(2*9)=18 ou

2*(2+3+4)=(2*2)+(2*3)+(2*4)=4+6+8=18

Sempre que um número multiplicar uma soma, ele irá multiplicar portanto cada parcela.

Divisão

Esse processo se dá quando desejamos dividir um total de produtos em partes iguais ou quando desejamos saber quantas vezes um número cabe dentro de outro.

* Exemplo 1

12/3=4

As divisões podem conter números exatos ou não. O resto do cálculo nesses casos, sempre deverá ser positivo e menor que o divisor. Caso isso não ocorra, a divisão não existe ou foi calculada de forma errada.

Exercícios resolvidos com as principais 4 operações matemáticas

1° (Adição)

a) 2+2=4

b) 5+1=6

c) 125+43=168

d) -2+(-5)=-7

e) -30+(-59)=-89

2° (Subtração)

a) 10-2=8

b) 4-3=1

c) 7-4=3

d) 100-103=-3

e) 24-30=-6

3° (Multiplicação)

a) 5*5=25

b) 10*2=20

c) 65*100=6.500

d) 2*(5+3)=16

e) 3*(7+2)=27

4° (Divisão)

a) 10/2=5

b) 100/25=4

c) 6/2=3

d) 36/6=6

e) 20/8=2,5